ABSTRACT
Keywords: SOIL, MOISTURE, FIELD CAPACITY, GENERAL CIRCULATION MODELS, CLIMATE, SIMULATION
1. Introduction
2. Why study soil moisture
- Soil moisture affects not only the vertical fluxes of energy and moisture, but also the horizontal fluxes of moisture, namely runoff. While atmospheric GCMs implemented in the AMIP experiment with specified SSTs can ignore runoff, these same models, with the same land surface parameterizations, are also being used in coupled land-ocean-atmosphere GCMs. One of the crucial connections between these three parts of the climate system is the thermohaline circulation of the ocean, which is driven in part by the fresh-water flux from the continents, the runoff. If the land surface parameterization does not produce the correct partitioning, the ocean circulation cannot be simulated correctly. If a 15-cm bucket model, or any other land surface parameterization, over high midlatitudes is always full because its field capacity is too small, it cannot properly simulate the month-to-month variations of runoff, and therefore it is important to evaluate the soil moisture per se, and not just the vertical fluxes.
- One of the most dire predictions of global warming is mid-latitude summer drought in the important agricultural regions of the Northern Hemisphere (Manabe et al., 1981; Houghton et al. 1996; Watson et al. 1996). Drought is a soil moisture deficiency. Plants care about the amount of soil moisture, not the fluxes. Therefore, evaluation of the ability of models to correctly simulate soil moisture is crucial to understand how well these models can calculate the impacts of global warming.
- Flooding is a soil moisture excess. Enhanced variability of climate has also been suggested as a result of global warming, with more flooding episodes (Houghton et al., 1996). In order to properly simulate this aspect of climate change, the soil moisture calculation must be correct.
- Any parameterization of physical quantities should be correct for the right physical reasons. In early versions of models, simple parameterizations may ignore some of the more complex physical interactions. For example, the original bucket model (Budyko, 1956) included partitioning of precipitation into runoff and infiltration, but ignored stomatal resistance to evapotranspiration. As implemented for the first time in a GCM by Manabe (1969), the partitioning was disabled and stomatal resistance was still missing. Some of the more complex parameterizations now include quite detailed treatment of runoff and evapotranspiration. It remains an open question as to whether this complexity results in improved simulations of soil moisture.
- Soil moisture, along with snow cover, is also the most important component of meteorological memory for the climate system over the land. Delworth and Manabe (1993) have shown that varying soil moisture (as opposed to fixed soil moisture) induces a redder spectrum in simulated climate by retaining the hydrological signature of anomalies for time scales longer than those of the atmosphere alone. Soil moisture anomalies should also be important for more accurate seasonal forecasts.
- Soil moisture variations from month to month are as large as the other terms in the hydrologic balance, namely precipitation, evaporation, and runoff, and correct simulation of these variations is necessary to correctly model the hydrological cycle.
3. Data sets
3.1. Scales of soil moisture variations
3.2. Observational data sets
3.3. Model-generated "data sets"
4. Soil moisture schemes
4.1. Calculated or prescribed soil moisture
4.2. Initialization
4.3. Prognostic variable
4.4. Field capacity
4.5. Number of soil layers
4.6. Vegetation
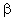 )
times the potential evaporation. In 9 of the schemes, vegetation
is considered explicitly, including the effects of canopy interception
and re-evaporation of precipitation, and stomatal resistance to
evapotranspiration. As pointed out by Dickinson et al. (1991),
in the absence of accurate atmospheric simulations of precipitation
and cloudiness, the inclusion of detailed canopy submodels may
not improve the results, and we find no evidence of such an improvement
for soil moisture simulations here.
)
times the potential evaporation. In 9 of the schemes, vegetation
is considered explicitly, including the effects of canopy interception
and re-evaporation of precipitation, and stomatal resistance to
evapotranspiration. As pointed out by Dickinson et al. (1991),
in the absence of accurate atmospheric simulations of precipitation
and cloudiness, the inclusion of detailed canopy submodels may
not improve the results, and we find no evidence of such an improvement
for soil moisture simulations here.
4.7. Runoff
5. Comparison of spatial fields
6. Comparison of seasonal cycles
7. Comparison of interannual variations and spinup problems
8. Discussion and conclusions
- The "data sets" of Mintz and Serafini (1981, 1989, 1992) and Schemm et al. (1992) are quite different from the observations. They also differ from each other by as much as 10 cm (out of a total of 15 cm) in the annual average over Asia, and by several cm in general over the rest of the world, even though they use the same calculation method.
- There is no evidence that more complicated models produce better simulations. Models which had multiple levels, or explicitly considered vegetation, or explicitly considered immediate or subsurface runoff did not produce better simulations of soil moisture than the bucket models. On the contrary, the SiBlings (JMA, COLA, and GLA) have time scales that are too long, especially in the regions with freezing temperatures.
- A field capacity of 15 cm is too low to capture high latitude soil moisture variations, in the AMIP models and the "data sets." The models with higher field capacities (ECMWF, MPI) do reproduce the observed patterns in these regions.
- There are large differences in the tropical model simulations of soil moisture. We do not have observations for this region to determine which are correct.
- All the winter soil moisture simulations in high latitudes produce constant soil moisture when the temperature is below freezing and the ground is snow covered, while observations show that soil moisture varies in the winter as much as in other seasons.
- Models begun without spinning up soil moisture produce long-term trends which can have serious effects on the first year or more of the simulations. These spinup problems probably contribute to the spinup errors in the surface air temperature fields shown by Mao and Robock (1997).
- The observed interannual variations of soil moisture in Illinois and Russia were not captured by any of the AMIP models. Because the month-to-month and interannual soil moisture anomalies are strongly controlled by precipitation and cloud cover anomalies, this implies that interannual variations of precipitation and cloudiness in these regions are controlled by factors in addition to the global sea surface temperature variations used to force the AMIP models.
9. Future progress
Budyko, M.I., 1956. Heat Balance of the Earth's Surface, Gidrometeoizdat, Leningrad, 255 pp. (in Russian)
Chen, T.H., Henderson-Sellers, A., Milly, P.C.D., Pitman, A.J., Beljaars, A.C.M., Polcher, J., Abramopolous, F., Boone, A., Chang, S., Chen, F., Dai, Y., Desborough, C.E., Dickinson, R.E., Dümenil, L., Ek, M., Garratt, J. R., Gedney, N., Gusev, Y. M., Kim, J., Koster, R., Kowalczyk, E.A., Laval, K., Lean, J., Lettenmaier, D., Liang, X., Mahfouf, J.-F., Mengelkamp, H.-T., Mitchell, K., Nasonova, O.N., Noilhan, J., Robock, A., Rosenzweig, C., Schaake, J., Schlosser, C.A., Schultz, J.-P., Shao, Y., Shmakin, A.B., Verseghy, D.L., Wetzel, P., Wood, E.F., Xue, Y., Yang, Z.-L., and Zeng, Q., 1997. Cabauw experimental results from the Project for Intercomparison of Land-surface Parameterization Schemes (PILPS). J. Climate, 10: 1194-1215.
Delworth, T., and Manabe, S., 1988. The influence of potential evaporation on the variabilities of simulated soil wetness and climate. J. Climate, 1: 523-547.
Delworth, T., and Manabe, S., 1993. Climate variability and land surface processes. Adv. Water Resources, 16: 3-20.
Desborough, C.E., 1997. The impact of root-weighting on the response of transpiration to moisture stress in a land surface scheme. Mon. Wea. Rev., in press.
Dickinson, R.E., Henderson-Sellers, A., Kennedy, P.J., and Wilson, M.F., 1986. Biosphere Atmosphere Transfer Scheme (BATS) for the NCAR Community Climate Model. NCAR Tech. Note NCAR/TN-387+STR, 72 pp.
Dickinson R.E., Henderson-Sellers, A., Rosenzweig, C., and Sellers, P.J. 1991. Evapotranspiration models with canopy resistance for use in climate models, a review. Agricultural and Forest Meteorol., 54: 373-388.
Douville, H., Royer, J.-F., and Mahfouf, J.F., 1995. A new snow parameterization for the Météo-France climate model, Part I: Validation in stand-alone experiments. Climate Dyn., 12: 21-35.
Douville, H., Royer, J.-F., and Mahfouf, J.F., 1995b. A new snow parameterization for the Météo-France climate model, Part II: Validation in a 3-D GCM experiment. Climate Dyn., 12: 37-52.
Gates, W. L., 1992. AMIP: the Atmospheric Model Intercomparison Project. Bull. Amer. Met. Soc., 73: 1962-1970.
Gleckler, P., Editor, 1997. AMIP II Guidelines, AMIP Newsletter No. 8, Lawrence Livermore National Laboratory, Livermore, California, 20 pp.
Henderson-Sellers, A., Editor, 1996a. Special Issue on Soil Moisture Simulation. Global Plan. Change, 13(1-4).
Henderson-Sellers, A., 1996b. Soil moisture: A critical focus for global change studies. Global Plan. Change, 13: 3-9.
Henderson-Sellers, A., Yang, Z.-L., and Dickinson, R.E., 1993. The Project for Intercomparison of Land-Surface Parameterization Schemes (PILPS). Bull. Amer. Met. Soc., 74: 1335-1349.
Hollinger, S.E., and Isard, S.A., 1994. A soil moisture climatology of Illinois. J. Climate, 7: 822-833.
Houghton, J.T., Meira Filho, L.G., Callander, B.A., Harris, N., Kattenberg, A., and Maskell, K., Editors, 1996. Climate Change 1995-The Science of Climate Change, Cambridge Univ. Press, Cambridge, 584 pp.
Jaeger, L. 1976: Monatskarten des Niederschlags fur die ganze Erde. Berichte Deutschen Wetterdienst 18 Nr 139, Offenbach, Germany.
Koster, R.D. and Milly, P.C.D., 1997. The interplay between transpiration and runoff formulations in land surface schemes used with atmospheric models. J. Climate, 10: 1578-1591.
Lau, K.M., Kim, J.H. and Sud, Y., 1996. Intercomparison of hydrologic processes in AMIP GCMs. Bull. Amer. Met. Soc., 77: 2209-2227.
Liston, G.E., Sud, Y.C., and Walker, G.K., 1993. Design of a Global Soil Moisture Initialization Procedure for the Simple Biosphere Model, NASA Tech. Mem. 104590, National Aeronautics and Space Administration, Greenbelt, Maryland, 138 pp.
Mahfouf, J.F., Manzi, A.O., Noilhan, J., Giordani, H., and Déqué, M., 1995. The land surface scheme ISBA within the Météo-France climate model ARPEGE. Part I: Implementation and preliminary results. J. Climate, 8: 2039-2057.
Manabe, S., 1969. Climate and the ocean circulation, 1. The atmospheric circulation and the hydrology of the earth's surface. Mon. Weather Rev., 97: 739-774.
Manabe, S., Wetherald, R.T., and Stouffer, R.J., 1981. Summer dryness due to increase of atmospheric CO2 concentration. Clim. Change, 3: 347-384.
Mao, J. and Robock, A., 1997. Surface air temperature simulations by AMIP general circulation models: Volcanic and ENSO signals and systematic errors. J. Climate, in press.
Meshcherskaya A.V., Boldyreva, N.A., and Shapaeva, N.D., 1982. Districts average plant available soil water storage and depth of snow cover. Statistical analysis and its usage (some examples). Gidrometeoizdat, Leningrad, 243 pp. (in Russian).
Mintz, Y., and Serafini, Y. 1981. Global fields of soil moisture and land-surface evapotranspiration. Research Review - 1980/81, NASA Goddard Space Flight Center Tech. Memo 83907, 178-180.
Mintz, Y., and Serafini, Y.V., 1989. Global monthly climatology of soil moisture and water balance. LMD Internal Report No. 148, Laboratoire de Météorologie Dynamique, Paris France, 102 pp.
Mintz, Y., and Serafini, Y.V., 1992. A global monthly climatology of soil moisture and water balance. Clim. Dyn., 8: 13-27.
Mocko, D.M. and Sud, Y.C., 1997. Comparison of a land-surface model (SSiB) to three parameterizations of evapotranspiration - a study based on ISLSCP Initiative I data. Submitted to J. Geophys. Res.
Noilhan, J. and Planton, S., 1989. A simple parameterization of land surface processes for meteorological models. Mon. Wea. Rev., 113: 1542-1553.
Phillips, T.J., 1994. A summary documentation of the AMIP models. PCMDI Report No. 18, Lawrence Livermore National Laboratory, Livermore, California, 343 pp. http://www-pcmdi.llnl.gov/modeldoc/amip
Pitman, A.J. , Henderson-Sellers, A., Abramopolous, F., Avissar, R., Bonan, G., Boone, A., Cogley, J.G., Dickinson, R.E., Ek, M., Entekhabi, D., Famiglietti, J., Garratt, J.R., Frech, M., Hahmann, A., Koster, R., Kowalczyk, E., Laval, K., Lean, J., Lee, T.J., Lettenmaier, D., Liang, X., Mahfouf, J.-F., Mahrt, L., Milly, P.C.D., Mitchell, K., deNoblet, N., Noilhan, J., Pan, H., Pielke, R., Robock, A., Rosenzweig, C., Running, S.W., Schlosser, C.A., Scott, R., Suarez, M., Thompson, S., Verseghy, D. L., Wetzel, P., Wood, E. F., Xue, Y., Yang, Z.-L. and Zhang, L., 1993. Results from off-line control simulations (Phase 1a), PILPS, GEWEX Report, IGPO Pub. Ser. 7, 47 pp.
Pitman, A.J., Henderson-Sellers, A., Abramopolous, F., Boone, A., Desborough, C.E., Dickinson, R.E., Garratt, J.R., Gedney, N., Koster, R., Kowalczyk, E.A., Lettenmaier, D., Liang, X., Mahfouf, J.-F., Noilhan, J., Polcher, J., Qu, W., Robock, A., Rosenzweig, C., Schlosser, C.A., Shmakin, A.B., Smith, J., Suarez, M., Verseghy, D.L., Wetzel, P., Wood, E.F., Xue, Y., and Yang, Z.-L., 1998. Key results and implications from Phase 1(c) of the Project for Intercomparison of Land-surface Parameterization Schemes. Submitted to Climate Dynamics.
Qu, W., Henderson-Sellers, A., Pitman, A.J., Chen, T.H., Abramopolous, F., Beljaars, A.C.M., Boone, A., Chang, S., Chen, F., Dai, Y., Desborough, C.E., Dickinson, R.E., Dümenil, L., Ek, M., Garratt, J.R., Gedney, N., Gusev, Y.M., Kim, J., Koster, R., Kowalczyk, E.A., Laval, K., Lean, J., Lettenmaier, D., Liang, X., Mahfouf, J.-F., Mengelkamp, H.-T., Milly, P.C.D., Mitchell, K., Nasonova, O.N., Noilhan, J., Polcher, J., Robock, A., Rosenzweig, C., Schaake, J., Schlosser, C.A., Schultz, J.-P., Shmakin, A.B., Verseghy, D.L., Wetzel, P., Wood, E.F., Xue, Y., Yang, Z.-L. andZeng, Q., 1998. Sensitivity of latent heat fluxes from PILPS land-surface schemes to perturbations of surface air temperature. J. Atmos. Sci., in press.
Randall, D.A., Sellers, P.J., Dazlich, D.A., Zhang, C., Collatz, G.J., Denning, A.S., Los, S.O., Field, C.B. and Fung, I., 1996. A revised land-surface parameterization (SiB2) for GCMs. Part III: The greening of the Colorado State University general circulation model, J. Climate, 9: 738-763.
Robock, A., Vinnikov, K.Y., Schlosser, C.A., Speranskaya, N.A. and Xue, Y., 1995a. Use of midlatitude soil moisture and meteorological observations to validate soil moisture simulations with biosphere and bucket models. J. Climate, 8: 15-35.
Robock, A., Schlosser, C.A., Vinnikov, K.Y., Liu, S. and Speranskaya, N.A., 1995b. Validation of humidity, moisture fluxes, and soil moisture in GCMs: report of AMIP Diagnostic Subproject 11; Part 1 - soil moisture. Proceedings of the First International AMIP Scientific Conference, WCRP-92, WMO/TD-No. 732, W. L. Gates, (Editor), World Climate Research Programme, Geneva, 85-90.
Robock, A., Vinnikov, K.Y., and Schlosser, C.A., 1997. Reply (Evaluation of land-surface parameterization schemes using observations). J. Climate, 10: 377-379.
Rodriguez-Iturbe, I., Vogel, G.K., Rigon, R., Entekhabi, D., Castelli, F. and Rinaldo, A., 1995. On the spatial organization of soil moisture fields. Geophys. Res. Lett., 22: 2757-2760.
Schemm, J., Schubert, S., Terry, J. and Bloom, S., 1992. Estimates of Monthly Mean Soil Moisture for 1979-1989. NASA Tech. Mem. 104571, National Aeronautics and Space Administration, Greenbelt, Maryland, 260 pp.
Schlosser, C.A., 1995. Land-Surface Hydrology: Validation And Intercomparison Of Multi-Year Off-Line Simulations Using Midlatitude Data. Ph.D. dissertation, Department of Meteorology, University of Maryland, College Park, 135 pp.
Schlosser, C.A., Robock, A., Vinnikov, K.Y., Speranskaya, N.A. and Xue, Y., 1997. 18-year land-surface hydrology model simulations for a midlatitude grassland catchment in Valdai, Russia. Mon. Weather Rev., in press.
Sellers, P.J., Mintz, Y., Sud, Y.C. and Dalcher, A., 1986: A simple biosphere model (SiB) for use within general circulation models. J. Atmos. Sci., 43: 505-531.
Sellers, P.J., Randall, D.A., Collatz, G.J., Berry, J.A., Field, C.B., Dazlich, D.A., Zhang, C., Collelo, G.D. and Bounoua, L., 1996a. A revised land-surface parameterization (SiB2) for GCMs. Part I: Model formulation, J. Climate, 9: 676-705.
Sellers, P.J., Los, S.O., Tucker, C.J., Justice, C.O., Dazlich, D.A., Collatz, C.J. and D.A. Randall, 1996b. A revised land-surface parameterization (SiB2) for GCMs. Part II: The generation of global fields of terrestrial biophysical parameters from satellite data, J. Climate, 9: 706-737.
Sellers, P.J., Dickinson, R.E., Randall, D.A., Betts, A.K., Hall, F.G., Berry, J.A., Collatz, G.J., Denning, A.S., Mooney, H.A., Nobre, C.A., Sato, N., Field, C.B. and Henderson-Sellers, A., 1997. Modeling the exchange of energy, water, and carbon between continents and the atmosphere. Science, 275: 502-509.
Sengupta, S. and Boyle, J.S., 1997. Comparing GCM Simulations, Ensembles and Model Revisions Using Common Principal Components, UCRL-JC-126621, PCMDI Report No. 40 Lawrence Livermore National Laboratory, Livermore, California, 32 pp.
Shao, Y. and Henderson-Sellers, A., 1996. Validation of soil moisture simulation in landsurface parameterisation schemes with HAPEX data. Glob. Plan. Change, 13: 11-46.
Slater, A.G., Pitman, A.J., andDesborough, C.E., 1997a. The simulation of freeze-thaw cycles in a GCM land surface scheme. Submitted to J. Geophys. Res.
Slater, A.G., Pitman, A.J. and Desborough, C.E., 1997b. The validation of a snow parameterization for use in general circulation models. Submitted to Int. J. Clim.
Spangler, W.M.L. and Jenne, R.L., 1984. Reference manual: World monthly surface station climatology. National Center for Atmospheric Research, Boulder, Colorado.
Thornthwaite, C.W., 1948. An approach toward a rational classification of climate. Geogr. Rev., 38: 55-94.
Vachaud G., Passerat de Silans, A., Balabanis, P., and Vauclin, M., 1985. Temporal stability of spatially measured soil water probability density function. Soil Sci. Soc. Am. J., 49: 822-828.
Vinnikov K.Y. and Yeserkepova, I.B., 1991. Soil moisture: empirical data and model results. J. Climate, 4: 66-79.
Vinnikov, K.Y., Robock, A., Speranskaya, N.A. and Schlosser, C.A., 1996. Scales of temporal and spatial variability of midlatitude soil moisture. J. Geophys. Res., 101: 7163-7174.
Viterbo, P. and Beljaars, A.C.M., 1995. An improved land surface parameterization scheme in the ECMWF model and its validation, J. Climate, 8: 2716-2748.
Watson, R.T., Zinyowera, M.C. and Moss, R.H. (Editors), 1996: Climate Change 1995-Impacts, Adaptations and Mitigation of Climate Change: Scientific-Technical Analyses, Cambridge Univ. Press, Cambridge, 880 pp.
Weare, B.C., Mokhov, I.I. and Project Members, 1995. Evaluation of total cloudiness and its variability in the Atmospheric Model Intercomparison Project, J. Climate, 8: 2224-2238.
Wetzel, P.J., Liang, X., Irannejad, P., Boone, A., Noilhan, J., Shao, Y., Skelly, C., Xue, Y. and Yang, Z.L., 1996. Modeling vadose zone liquid water fluxes: Infiltration, runoff, drainage, interflow. Glob. Plan. Change, 13: 57-71.
Xue, Y., Sellers, P.J., Kinter, J. L. and Shukla, J., 1991: A simplified biosphere model for global climate studies. J. Climate, 4: 345-364.
Xue, Y., Zeng, F.J. and Schlosser, C.A., 1996. SSiB and its sensitivity to soil propertiesa case study using HAPEX-Mobilhy data. Glob. Plan. Change, 13: 183-194.
Yang, Z.-L., Dickinson, R.E., Robock, A. and Vinnikov, K.Y., 1997. On validation of the snow sub-model of the Biosphere-Atmosphere Transfer Scheme with Russian snow cover and meteorological observational data. J. Climate, 10: 353-373.
1. Calculated or prescribed soil moisture
2. Initialization: climatology or previous model solution
3. Available (bucket) or total (SiBling) soil moisture
4. Field capacity (12 - 212.5 cm)
5. Number of levels (0 - 6)
6. Vegetation: implicit (
7. Runoff: bucket overflow
V with explicit vegetation (canopy interception
and stomatal resistance)
** cm of plant-available soil moisture
for the entire soil depth
* with prescribed deep soil moisture
§ not in Standard Output
Models with climatological initialization (Phillips, 1994), but
which appear to be balanced initially:
Models with initialization from a previous model solution (Phillips,
1994), but which appear to not be balanced initially:
Models with climatological initialization (Phillips, 1994) and
which are imbalanced initially:
Figure 1. Schematic diagram of hydrological and meteorological
scales of soil moisture variations. r is the autocorrelation
function. The scales are determined by the slopes of the curves:
for time scales,
Figure 2. Observed available soil moisture (cm) in the top 1
m, averaged for 1979-1988 for Russia. Station locations are indicated
by the circles. The box shows the region used for the comparison
of models and observations in Figs. 12-13.
Figure 3. Observed available soil moisture (cm) in the top 1
m, averaged for 1979-1988 for Illinois, USA. Observations started
in 1981. Station locations are indicated by the circles. The
box shows the region used for the comparison of models and observations
in Figs. 12-13.
Figure 4. Comparison of Mintz and Serafini (1981, 1989, 1992)
and Schemm et al. (1992) "data sets" with each other
and with observations.
Figure 5. Annual average of prescribed soil moisture fields for
the 3 models for which this variable was provided to the AMIP
Standard Output. Note that NCAR and NRL are in unspecified units,
presumably on scales of 0-10 and 0-1 of wetness fractions. GSFC
is in cm of plant-available soil moisture in the top 1 m of soil.
Figure 6. Observed field capacity for Russian stations. The
stations with red circles often have measured available soil moisture
that exceeds the field capacity, while for those circled in blue,
the field capacity always exceeds the measured available soil
moisture.
Figure 7. Annual average of plant-available soil moisture fields
for 6 of the models with standard 15-cm buckets. Units are in
cm of plant-available soil moisture in the top 1 m of soil.
Figure 8. Annual average of plant-available soil moisture fields
for 4 of the models with standard 15-cm buckets, one with a 12-cm
bucket and one with a 16.2-cm bucket. Units are in cm of plant-available
soil moisture in the top 1 m of soil.
Figure 9. Annual average of wetness (plant-available soil moisture
divided by field capacity) for 3 of the models which only provided
soil moisture for the top layer, and for 2 models with large field
capacities. Shown are wetness only for those top layers (MRI,
SUNYA/NCAR, UGAMP) and for the entire soil layer (ECMWF, MPI).
Figure 10. Annual average of total soil moisture (cm) for the
3 SiBlings and for GISS. The depth of the soil layer varies spatially.
For the COLA model, the plant-available soil moisture is also shown.
Figure 11. Annual average of plant-available soil moisture fields
for 4 of the models with unknown variable field capacities. Units
are in cm of plant-available soil moisture.
Figure 12. Seasonal cycle of soil moisture (cm) averaged for
the last 9 years of the AMIP simulations for all models and for
observations for 2 different boxes where we have observations,
a) Russia (Fig. 2) and
b) Illinois (Fig. 3). For the models,
the monthly average is plotted. For the observations, data from
the first day of the month are plotted.
Figure 13. Soil moisture anomalies (cm) with respect to the monthly
means for 1980-1989 for all models and for observations, averaged
for same regions as in Fig. 12.
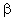 x potential
evaporation), or
x potential
evaporation), or
Acronym AMIP Group
Location BMRC Bureau of Meteorology Research Centre
Melbourne, Australia CCC Canadian Centre for Climate Modelling and Analysis
Victoria, Canada CNRM Centre National de Recherches Météorologiques
Toulouse, France COLA Center for Ocean-Land-Atmosphere Studies
Calverton, Maryland (USA) CSIRO Commonwealth Scientific & Industrial Research Organization
Mordialloc, Australia CSU Colorado State University
Fort Collins, Colorado (USA) DERF Dynamical Extended Range Forecasting(at GFDL)
Princeton, New Jersey (USA) DNM Department of Numerical Mathematics(of the Russian Academy of Sciences)
Moscow, Russia ECMWF European Centre for Medium-Range Weather Forecasts
Reading, England GFDL Geophysical Fluid Dynamics Laboratory
Princeton, New Jersey (USA) GISS Goddard Institute for Space Studies
New York, New York (USA) GLA Goddard Laboratory for Atmospheres
Greenbelt, Maryland (USA) GSFC Goddard Space Flight Center
Greenbelt, Maryland (USA) IAP Institute of Atmospheric Physics(of the Chinese Academy of Sciences)
Beijing, China JMA Japan Meteorological Agency
Tokyo, Japan LMD Laboratoire de Météorologie Dynamique
Paris, France MGO Main Geophysical Observatory
St. Petersburg, Russia MPI Max-Planck-Institut für Meteorologie
Hamburg, Germany MRI Meteorological Research Institute
Ibaraki-ken, Japan NCAR National Center for Atmospheric Research
Boulder, Colorado (USA) NMC National Meteorological Center
Suitland, Maryland (USA) NRL Naval Research Laboratory
Monterey, California (USA) RPN Recherche en Prévision Numérique
Dorval, Canada SUNYA State University of New York at Albany
Albany, New York (USA) SUNYA/ State University of New York at Albany/
Albany, New York (USA)/ NCAR National Center for Atmospheric Research
Boulder, Colorado (USA) UCLA University of California at Los Angeles
Los Angeles, California (USA) UGAMP The UK Universities' Global Atmospheric Modelling Programme
Reading, England
UIUC University of Illinois at Urbana-Champaign
Urbana, Illinois (USA) UKMO United Kingdom Meteorological Office
Bracknell, United Kingdom YONU Yonsei University
Seoul, Korea
CNRM
DNM*, GFDL, IAP, LMD, SUNYA, YONU
CSIRO
CCCV, MGO, UIUC, UKMOV
MRI
BMRC, CSU, DERF, NMCV
MPIV
ECMWFV*, UGAMP*
SNG (LSX)V
GLA (SSiB)V, GISSV
COLA (SSiB)V, JMA (SiB)V
GSFC, NCAR, NRL, RPN§, UCLA§
0 1
2 3 4
5 6
GSFC BMRC CNRM
COLA MRI
GISS NCAR CCC CSIRO
ECMWF
SUNYA/NCAR NRL CSU DNM
GLA
RPN DERF MGO
JMA
UCLA GFDL
UGAMP
IAP
LMD
MPI
NMC
SUNYA
UIUC
UKMO
YONU
Explicit (canopy interception,
Implicit (b x PE)
stomatal resistance)
BMRC CCC COLA
ECMWF CNRM CSIRO GISS
GLA CSU DERF JMA
MPI DNM GFDL NMC*
SUNYA/NCAR GSFC IAP UKMO
LMD MGO * no canopy interception
MRI NCAR NRL RPN SUNYA UCLA
UGAMP UIUC
YONU
None Bucket Overflow
Bucket Overflow Bucket Overflow
(Prescribed W) Only
plus Immediate Fraction
plus Immediate Fraction from Precipitation
from Precipitation
plus Deep Subsurface GSFC BMRC CSIRO
COLA NCAR CCC ECMWF
GISS NRL CNRM IAP
GLA RPN CSU MGO
JMA UCLA DERF MRI
MPI DNM UIUC
SUNYA/NCAR GFDL YONU
UKMO LMD NMC SUNYA UGAMP
 , t is time and
T is the time scale; for spatial scales,
, t is time and
T is the time scale; for spatial scales,  ,
d is distance and L is the length scale.
,
d is distance and L is the length scale.